library(haven)
library(tidyverse)
pisa_idn <- read_csv("pisa_idn.csv")
skor <- pisa_idn %>% select(ST184Q01HA, ST185Q01HA, ST185Q02HA, ST185Q03HA, ST034Q01TA,PV1MATH,PV2MATH,PV3MATH,PV4MATH,PV5MATH,
PV6MATH, PV7MATH, PV8MATH, PV9MATH, PV10MATH, CNTSTUID, CNTSCHID, CNTRYID) %>%
filter(CNTSCHID == 36000271 |
CNTSCHID == 36000272 |
CNTSCHID == 36000273 |
CNTSCHID == 36000274 |
CNTSCHID == 36000275 |
CNTSCHID == 36000276 |
CNTSCHID == 36000277 |
CNTSCHID == 36000278 |
CNTSCHID == 36000279 |
CNTSCHID == 36000280 |
CNTSCHID == 36000285 |
CNTSCHID == 36000286 |
CNTSCHID == 36000287 |
CNTSCHID == 36000288 |
CNTSCHID == 36000289 |
CNTSCHID == 36000290 |
CNTSCHID == 36000291 |
CNTSCHID == 36000292 |
CNTSCHID == 36000293 |
CNTSCHID == 36000294) %>%
mutate(math=(PV1MATH+PV2MATH+PV3MATH+PV4MATH+PV5MATH+
PV6MATH+PV7MATH+PV8MATH+PV9MATH+PV10MATH)/10) %>%
mutate(growth1=recode(ST184Q01HA, "1" = "4", "2" = "3", "3" = "2", "4"="1")) %>%
mutate(sekolah=CNTSCHID) %>%
mutate(growth=ST184Q01HA)10 Analisis Multilevel
10.1 Motivasi
- Data besar/sekunder dalam R
- Insight psikologi untuk kebijakan
- Penggunaan R
10.2 Outline
- Mengapa multilevel?
- Konsep utama analisis multilevel
- Ilustrasi estimasi multilevel
- Penerapan dan refleksi
10.3 Annual Reviews of Psychology

10.4 Mengapa analisis multilevel?
Pemodelan regresi klasik mengasumsikan bahwa kasus adalah independen. Hal ini tidak selalu benar ketika kita menjumpai struktur tersarang. Misalnya, siswa yang bersekolah di sekolah yang sama mungkin memiliki hasil yang serupa (atau lebih mirip daripada sampel acak).
Jadi, dalam situasi ini asumsi regresi OLS tidak terpenuhi, mengabaikan struktur tersarang akan menyebabkan hasil yang bias.
Analisis statistik standar sangat bergantung pada asumsi independensi pengamatan. Jika asumsi ini dilanggar (pada data tersarang) maka standar error terlalu kecil dan menghasilkan banyak hasil signifikansi yang kurang tepat.
10.5 Mengapa analisis multilevel?
Struktur tersarang ini bisa memberi tahu kita hal-hal penting tentang dunia sosial. Mengetahui berapa banyak variasi yang kita miliki di setiap tingkat dapat menginformasikan kebijakan dan teori.
Model multilevel memungkinkan kita untuk memperkirakan sumber variasi yang berbeda ini.
10.6 Mengapa Analisis Multilevel?
10.7 Penelitian multilevel
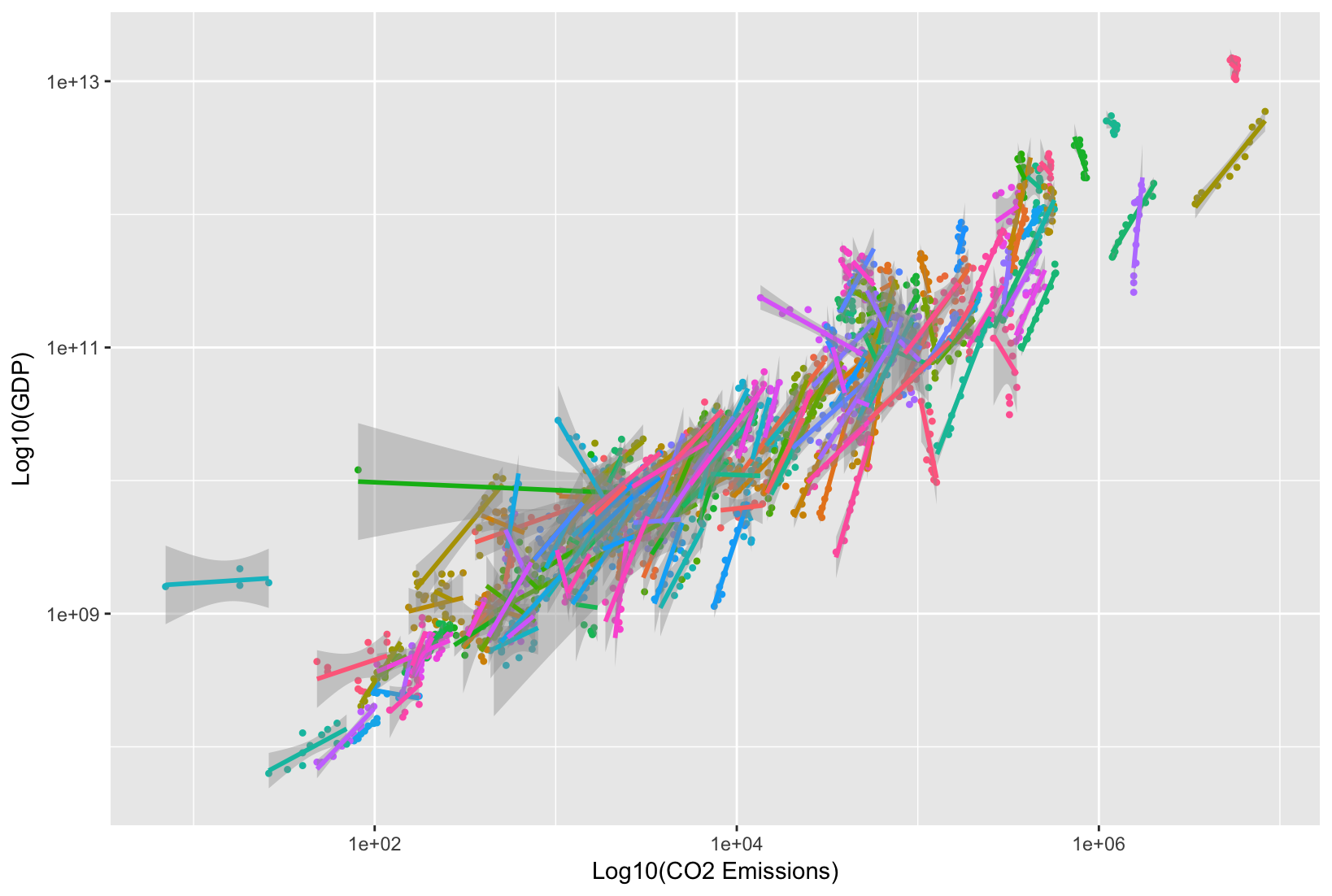
Penelitian sosial seringkali melibatkan masalah terkait menyelidiki hubungan antara individu dan konteks sosial tempat mereka tinggal, bekerja , atau belajar.
Asumsi dasarnya adalah individu berinteraksi dengan konteks sosial tempat mereka berada, individu dipengaruhi oleh konteks atau kelompok di mana mereka berasal , dan bahwa kelompok tersebut pada gilirannya dipengaruhi oleh individu yang membentuk kelompok itu .
Individu dan kelompok sosial dikonseptualisasikan sebagai sistem hierarki individu yang tersarang dalam kelompok, dengan individu dan kelompok ditentukan pada level terpisah dari sistem hierarki ini .
Secara alami, sistem seperti itu dapat diamati pada level hierarki yang berbeda, dan variabel dapat ditentukan di setiap level.
Hal ini mengarah pada penelitian tentang hubungan antara variabel yang menjadi ciri individu dan variabel yang mencirikan kelompok. Penelitian ini disebut sebagai penelitian multilevel
10.8 Data tersarang
- Struktur data bertingkat adalah struktur di mana pengamatan pada satu tingkat analisis disarangkan (atau dikelompokkan atau dikelompokkan) dalam pengamatan pada tingkat analisis lainnya.
- Struktur data bertingkat digambarkan hanya sebagai bersarang atau bersarang secara hierarkis.
- Fitur penting dan menentukan dari data multilevel tersebut adalah bahwa pengamatan pada satu tingkat analisis tidak independen satu sama lain—ada saling ketergantungan di antara data yang perlu diperhitungkan.
10.9 Ilustrasi
10.10 Intuisi analisis multilevel
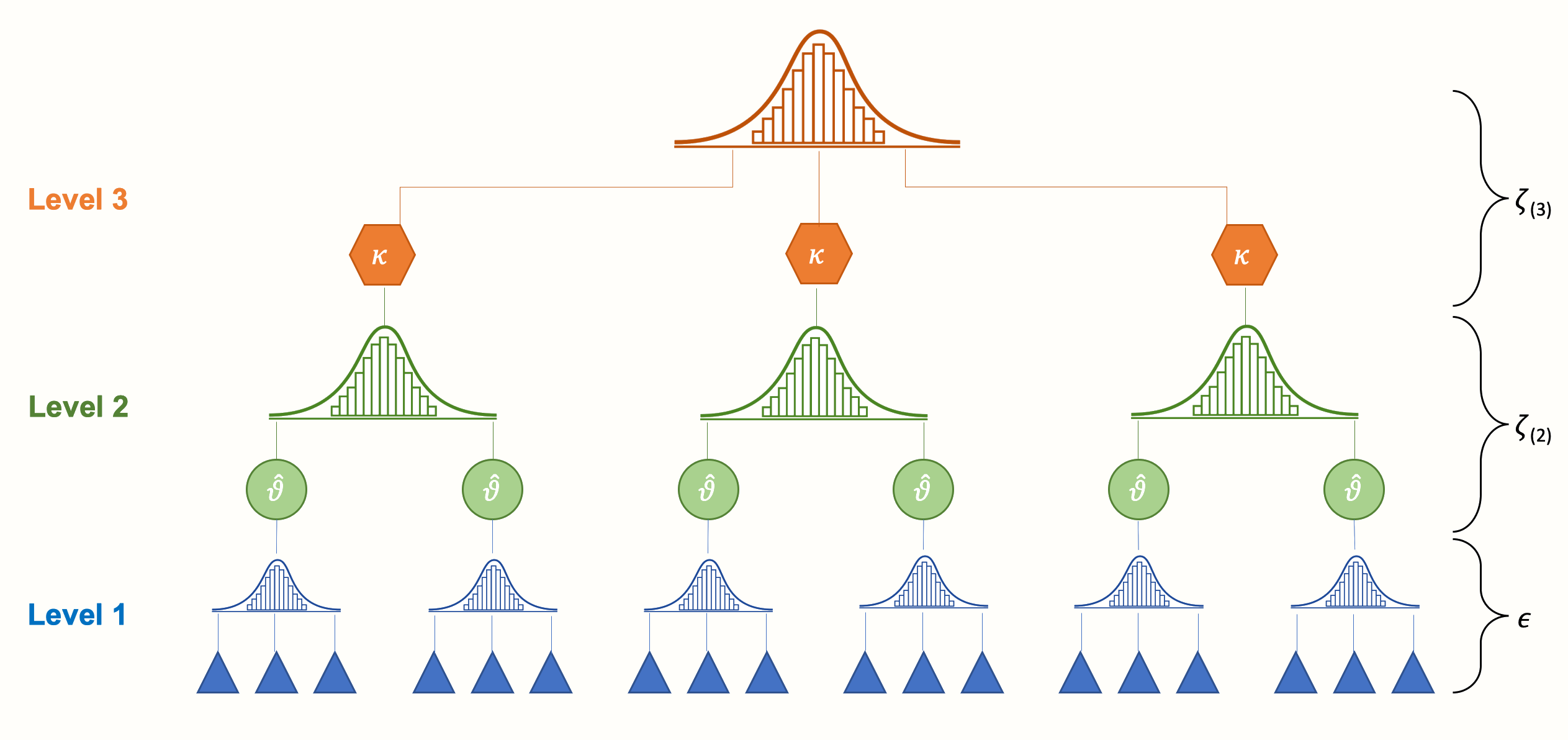
- Dalam model bertingkat kita memisahkan sumber variasi.
- Dalam konteks saat kita memisahkan informasi tingkat siswa dan sekolah sehingga kita memiliki dua sumber variasi yang berbeda.
- Dalam proses estimasi kita mulai dengan model null sehingga kita memiliki referensi dan memahami berapa banyak variasi yang dimiliki pada setiap level.
10.11 Multilevel model
Yij = γ00 + U0j + Rij
- Yij: variabel tergantung yang bervariasi secara individual i, pada kelompok j.
- γ00: intercept
- U0j: variasi antar kelompok. Memberi informasi bahwa kelompok berbeda satu sama lain.
- Rij: variasi individual. Koefisien ini memberi informasi perbedaan individu setiap kelompok.
10.12 Random Intercept
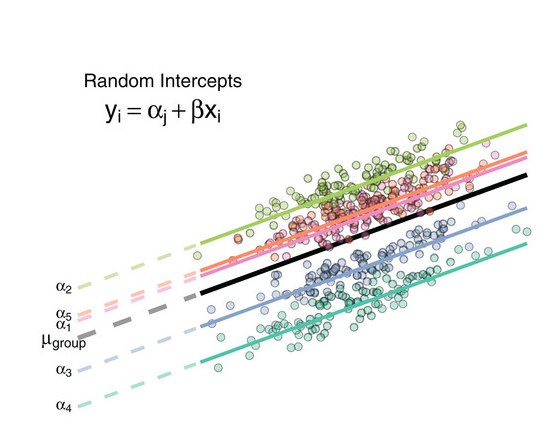
10.13 Random Slope
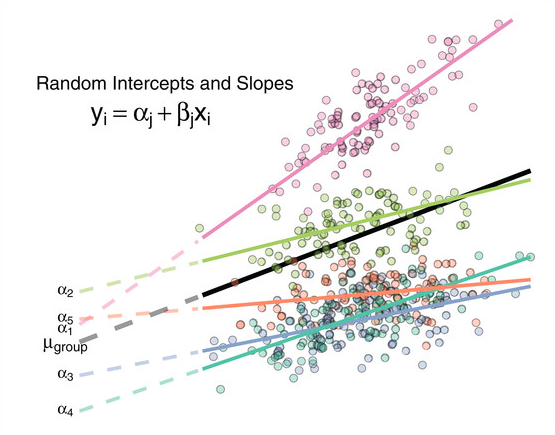
10.14 Intraclass correlation (ICC) 1
- Dalam kasus di mana individu dikelompokkan atau bersarang dalam unit level yang lebih tinggi misal: kelas , sekolah , distrik sekolah), dimungkinkan untuk memperkirakan korelasi antara skor individu dalam cluster/struktur bersarang menggunakan korelasi intraklass 𝜌).
- 𝜌 adalah ukuran proporsi variasi dalam variabel hasil yang terjadi antara grup versus variasi total yang ada.
10.15 Intraclass correlation (ICC) 2
Nilai 𝜌 berkisar dari 0 (tidak ada variansi antar grup) hingga 1 (variansi antar grup).
Nilai 𝜌 yang tinggi mengindikasikan bahwa sumbangan besar dari variasi total dalam ukuran hasil dikaitkan dengan keanggotaan grup; yaitu ada hubungan yang relatif kuat antara skor untuk dua individu dari kelompok yang sama ⟹individu dalam grup yang sama (misalnya sekolah) lebih mirip pada variabel terukur daripada individu yang berada di kelompok lain.
10.16 Intraclass correlation (ICC) 3
ICC adalah alat penting dalam pemodelan multilevel, karena ICC merupakan indikator sejauh mana struktur data multilevel dapat mempengaruhi variabel hasil yang diinginkan.
Nilai ICC yang lebih besar menunjukkan dampak pengelompokan yang lebih besar. Berarti semakin tinggi nilai ICC maka semakin penting penggunaan analisis multilevel.
10.17 PISA Indonesia
Growth mindset dan skor matematika
20 sekolah
700+ siswa
10.18 Jumlah siswa per sekolah
skor <- skor %>% filter(growth != "NA")
knitr::kable(count(skor, CNTSCHID))| CNTSCHID | n |
|---|---|
| 36000271 | 21 |
| 36000272 | 39 |
| 36000273 | 40 |
| 36000274 | 29 |
| 36000275 | 39 |
| 36000276 | 35 |
| 36000277 | 30 |
| 36000278 | 38 |
| 36000279 | 40 |
| 36000280 | 36 |
| 36000285 | 38 |
| 36000286 | 39 |
| 36000287 | 39 |
| 36000288 | 38 |
| 36000289 | 39 |
| 36000290 | 40 |
| 36000291 | 40 |
| 36000292 | 39 |
| 36000293 | 36 |
| 36000294 | 38 |
10.19 Ringkasan Statistik
skor %>%
group_by(CNTSCHID) %>%
summarise(mean = mean(math, na.rm = T),
SD = sd(math, na.rm = T),
miss = mean(is.na(math))) %>%
mutate_if(is.numeric, ~round(., 2)) %>%
print(n = 50)# A tibble: 20 × 4
CNTSCHID mean SD miss
<dbl> <dbl> <dbl> <dbl>
1 36000271 328. 49.4 0
2 36000272 506. 43.4 0
3 36000273 425. 59.8 0
4 36000274 302. 39.4 0
5 36000275 479. 48.4 0
6 36000276 325. 41.6 0
7 36000277 367. 42.3 0
8 36000278 437. 42.4 0
9 36000279 347. 56.6 0
10 36000280 343. 47.4 0
11 36000285 454. 33.2 0
12 36000286 500. 41.8 0
13 36000287 422. 51.0 0
14 36000288 371. 73.7 0
15 36000289 307. 54.8 0
16 36000290 393. 64.2 0
17 36000291 442. 54.2 0
18 36000292 475. 44.3 0
19 36000293 362. 48.8 0
20 36000294 381. 60.8 011 Model Regresi
11.1 Model regresi
m <- lm(math~ 1, data = skor)
d <- coef(summary(m))
knitr::kable(d)| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 402.3658 | 2.963256 | 135.785 | 0 |
11.2 Garis regresi
p1 <- ggplot(data = skor, aes(x=growth, y = math, color = CNTSCHID))+ xlim(1,4)+
geom_point()+
geom_jitter() +
geom_smooth(method="lm", se = FALSE)+
theme_bw()
print(p1)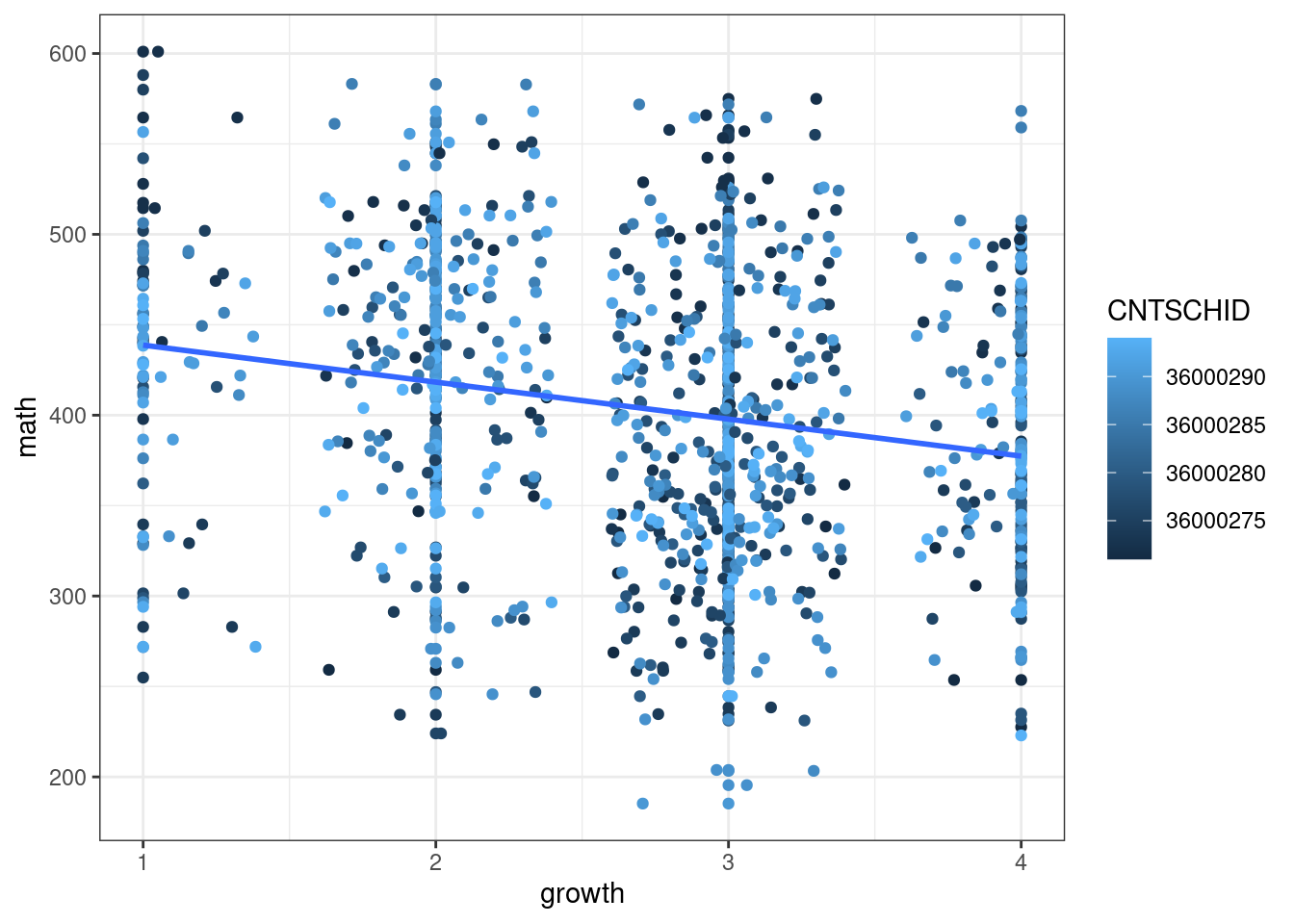
11.3 Sebaran Skor Matematika per sekolah
skor %>%
ggplot(aes(math)) +
geom_density() +
facet_wrap(~CNTSCHID)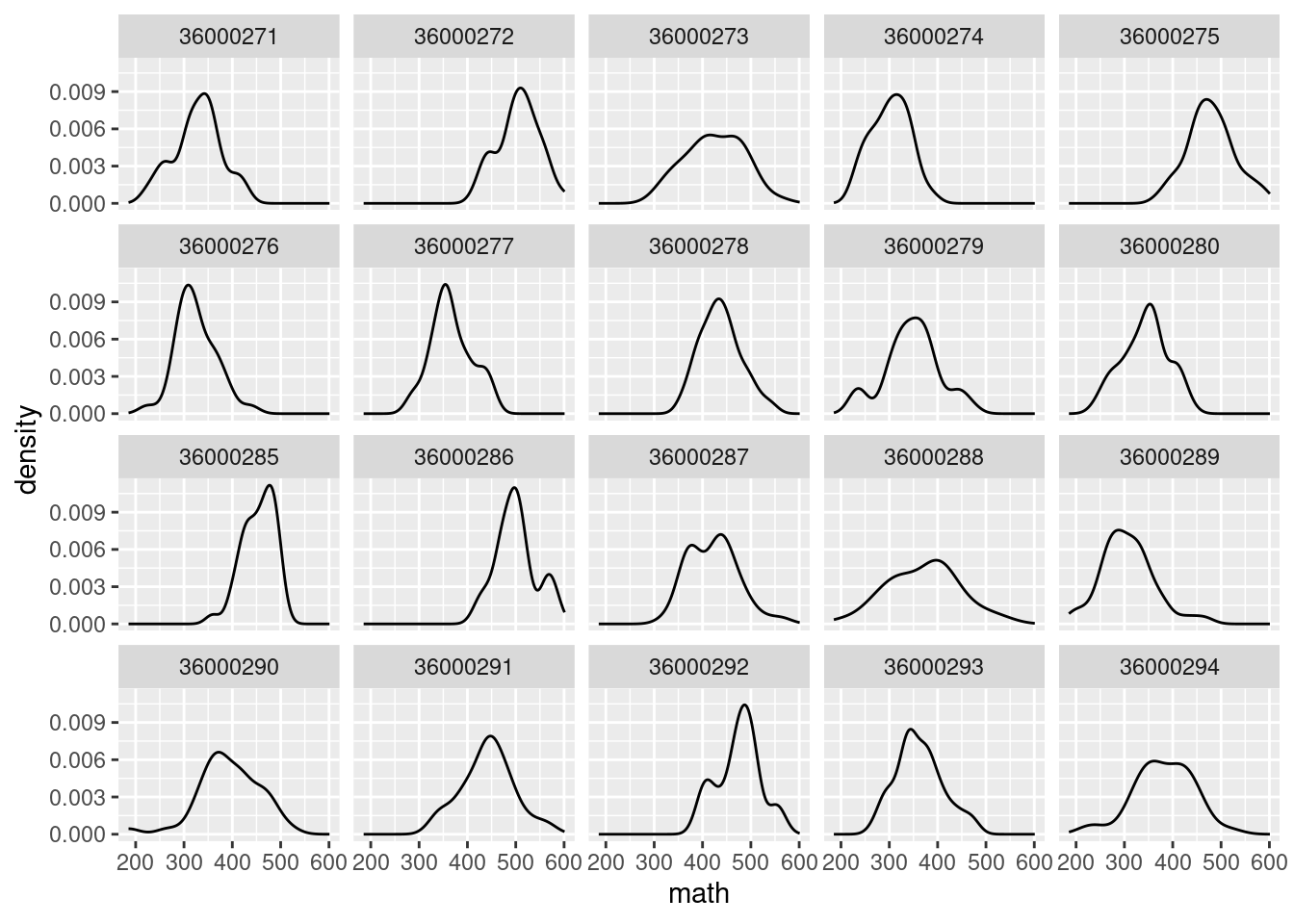
11.4 Distribusi Growth Mindset per sekolah
skor %>%
ggplot(aes(growth)) +
geom_bar() +
facet_wrap(~CNTSCHID)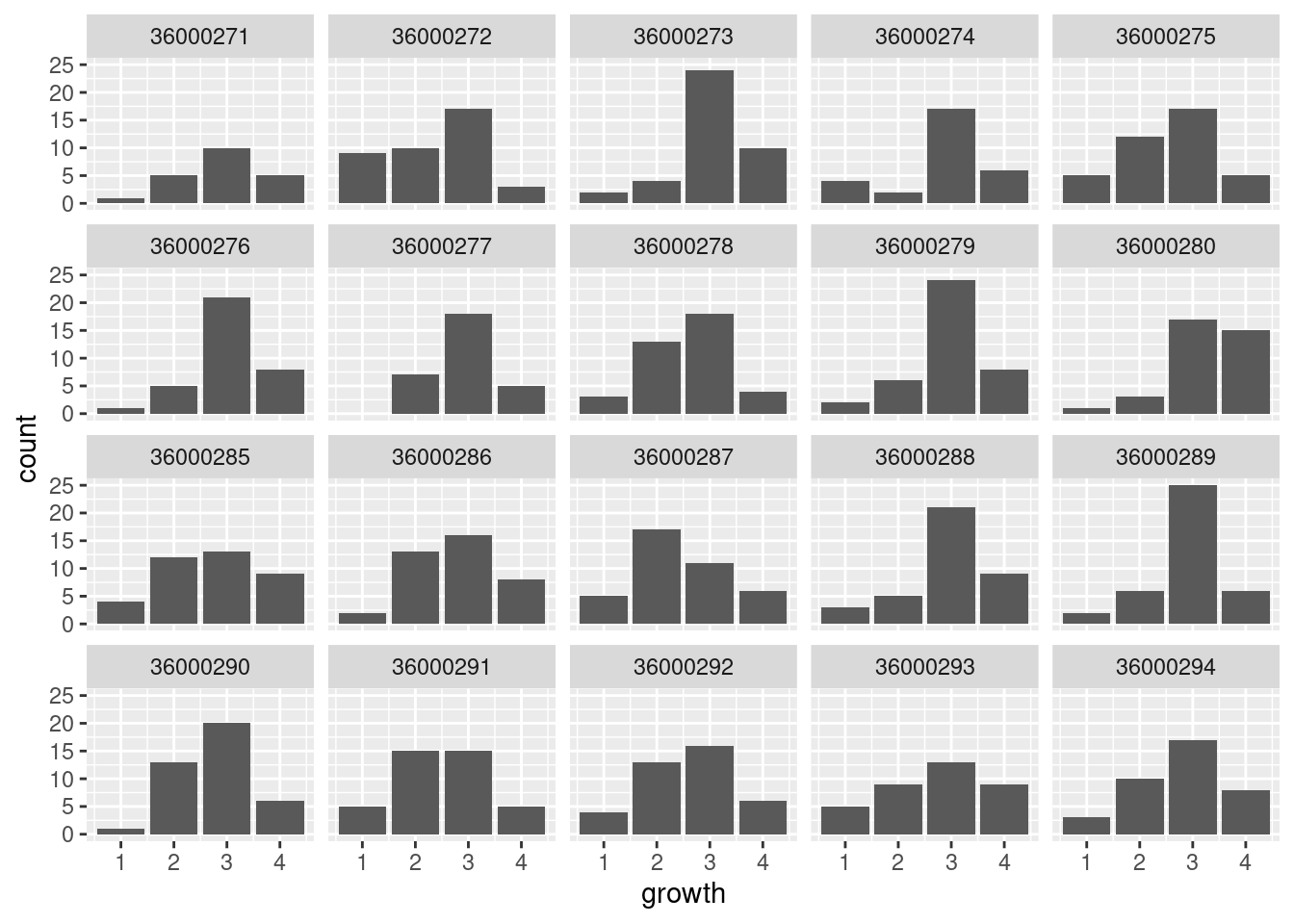
12 Model Null
12.1 Estimasi Model Null
12.2 Model Null
tab_model(m0)| math | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 398.31 | 369.99 – 426.63 | <0.001 |
| Random Effects | |||
| σ2 | 2613.86 | ||
| τ00 CNTSCHID | 4088.60 | ||
| ICC | 0.61 | ||
| N CNTSCHID | 20 | ||
| Observations | 733 | ||
| Marginal R2 / Conditional R2 | 0.000 / 0.610 | ||
12.3 Interpretasi Model Null
398.31 adalah intercept atau nilai yang diharapkan (i.e. rata-rata) dari skor matematika pada semua sekolah dan siswa.
4089 adalah varisi sekolayh dalam skor matematika
2614 adalah individual level variation dalam skor matematika
12.4 Distribusi per sekolah
# save predicted scores
skor$m0 <- predict(m0)
# graph with predicted country level support for immigration
skor %>%
ggplot(aes(math, m0, color = CNTSCHID, group = CNTSCHID)) +
geom_smooth(se = F, method = lm) +
geom_jitter()+
theme_bw() +
theme(axis.text.x = element_blank(),
axis.ticks = element_blank()) +
labs(x = "", y = "Skor Matematika", color = "Sekolah")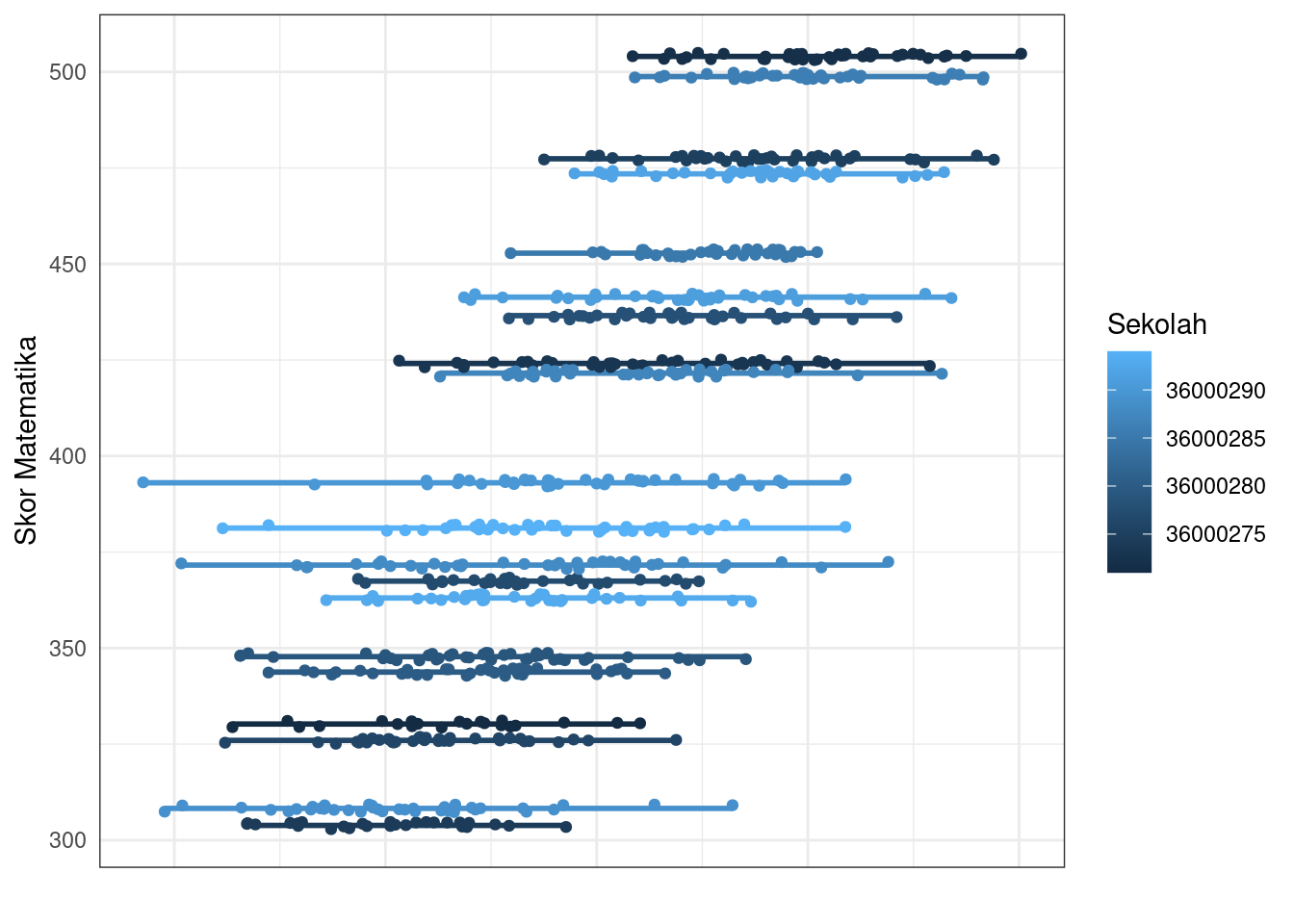
Variasi di tingkat sekolah dapat dilihat seberapa panjang garis. Jika pendek relatif sama, sedangkan jika panjang, relatif berbeda. Variasi tingkat individu adalah ringkasan perbedaan antara setiap individu dilihat jarak dari titik ke garis.
12.5 Interpretasi ICC Model Null
ICC<-4089/(4089+2614)
print(ICC)[1] 0.6100254- 61% variasi dalam skor matematika berasal dari sekolah atau 39% disebabkan oleh karakteristik siswa.
- jika kita memilih siswa dari sekolah yang sama, korelasi yang diharapkan dalam skor matematika adalah 0,61.
12.6 Sebaran intercept
## Lattice
# dotplot using lattice package
library(lattice)
qqmath(ranef(m0, condVar = TRUE))$CNTSCHID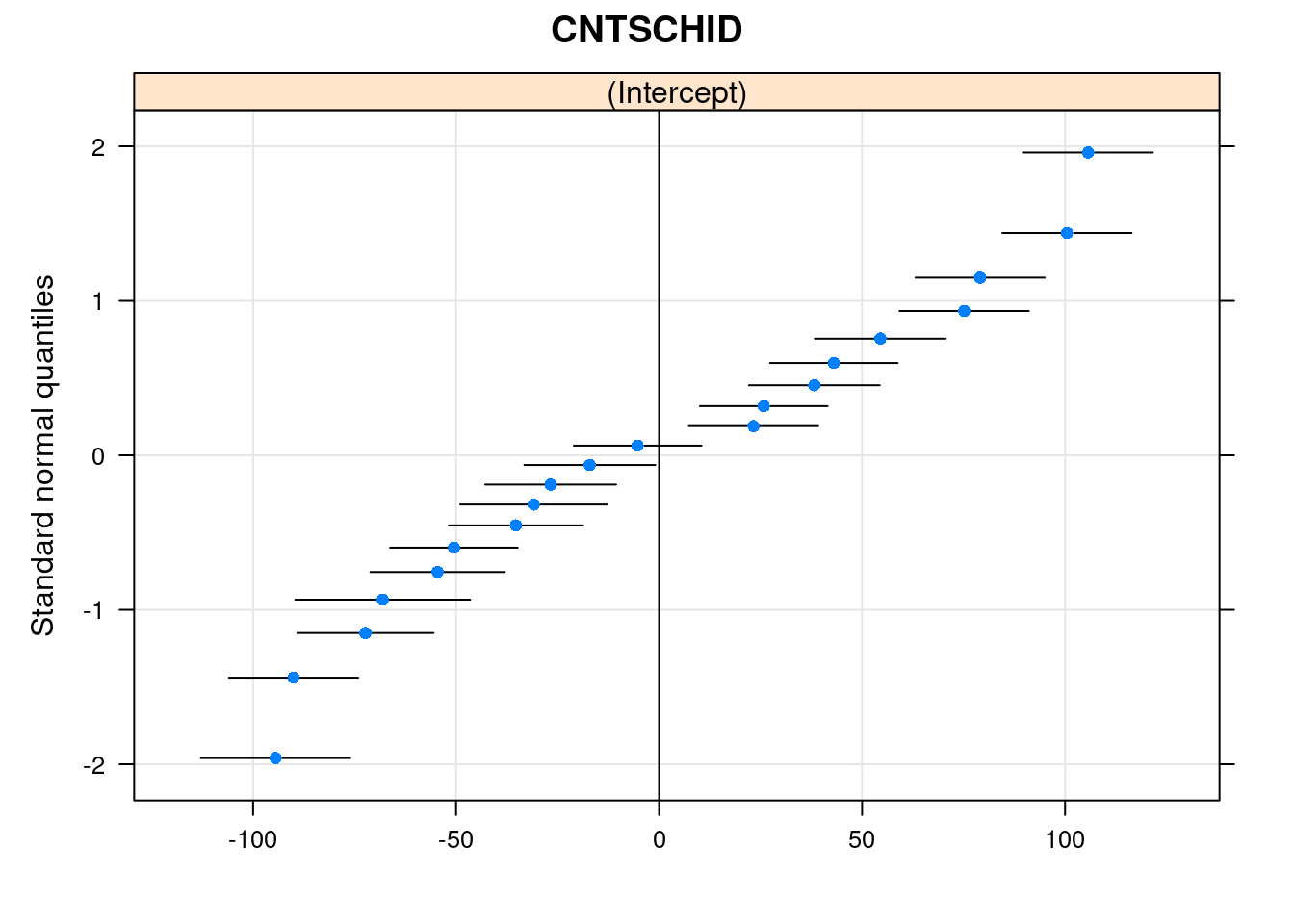
Dalam grafik ini setiap titik mewakili suatu sekolah dan garis di sekitarnya adalah interval kepercayaan.
13 Random Intercept
13.1 Estimasi Random Intercept
# random intercept with a control variable
m1 <- lmer(math ~ 1 + growth + (1 | CNTSCHID), data = skor)
summary(m1)Linear mixed model fit by REML ['lmerMod']
Formula: math ~ 1 + growth + (1 | CNTSCHID)
Data: skor
REML criterion at convergence: 7904.4
Scaled residuals:
Min 1Q Median 3Q Max
-4.0598 -0.6458 0.0304 0.6155 3.1288
Random effects:
Groups Name Variance Std.Dev.
CNTSCHID (Intercept) 3930 62.69
Residual 2573 50.73
Number of obs: 733, groups: CNTSCHID, 20
Fixed effects:
Estimate Std. Error t value
(Intercept) 421.196 15.500 27.17
growth -8.213 2.275 -3.61
Correlation of Fixed Effects:
(Intr)
growth -0.40913.2 Estimasi Random Intercept
library(sjPlot)
tab_model(m1)| math | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 421.20 | 390.77 – 451.63 | <0.001 |
| growth | -8.21 | -12.68 – -3.75 | <0.001 |
| Random Effects | |||
| σ2 | 2573.19 | ||
| τ00 CNTSCHID | 3929.81 | ||
| ICC | 0.60 | ||
| N CNTSCHID | 20 | ||
| Observations | 733 | ||
| Marginal R2 / Conditional R2 | 0.007 / 0.607 | ||
13.3 ICC Random Intercept
ICC2=3930/(3930+2573)
print(ICC2)[1] 0.604336513.4 Interpretasi Random Intercept
- Bertambahnya 1 poin growth mindset, skor matematika meningkat sebesar 8,21.
- ICC sedikit lebih kecil dibandingkan dengan model sebelumnya.
- Growth mindset dapat sedikit menjelaskan variasi skor matematika baik di tingkat siswa maupun sekolah.
13.5 Sebaran Model 1 (Random Intercept)
# save predicted scores
skor$m1 <- predict(m1)
# plot lines based on our model
skor %>%
ggplot(aes(growth, m1, color = CNTSCHID, group = CNTSCHID)) +
geom_smooth(se = F, method = lm) +
geom_jitter()+
theme_bw() +
labs(x = "Growth Mindset",
y = "Skor Matematika",
color = "Sekolah")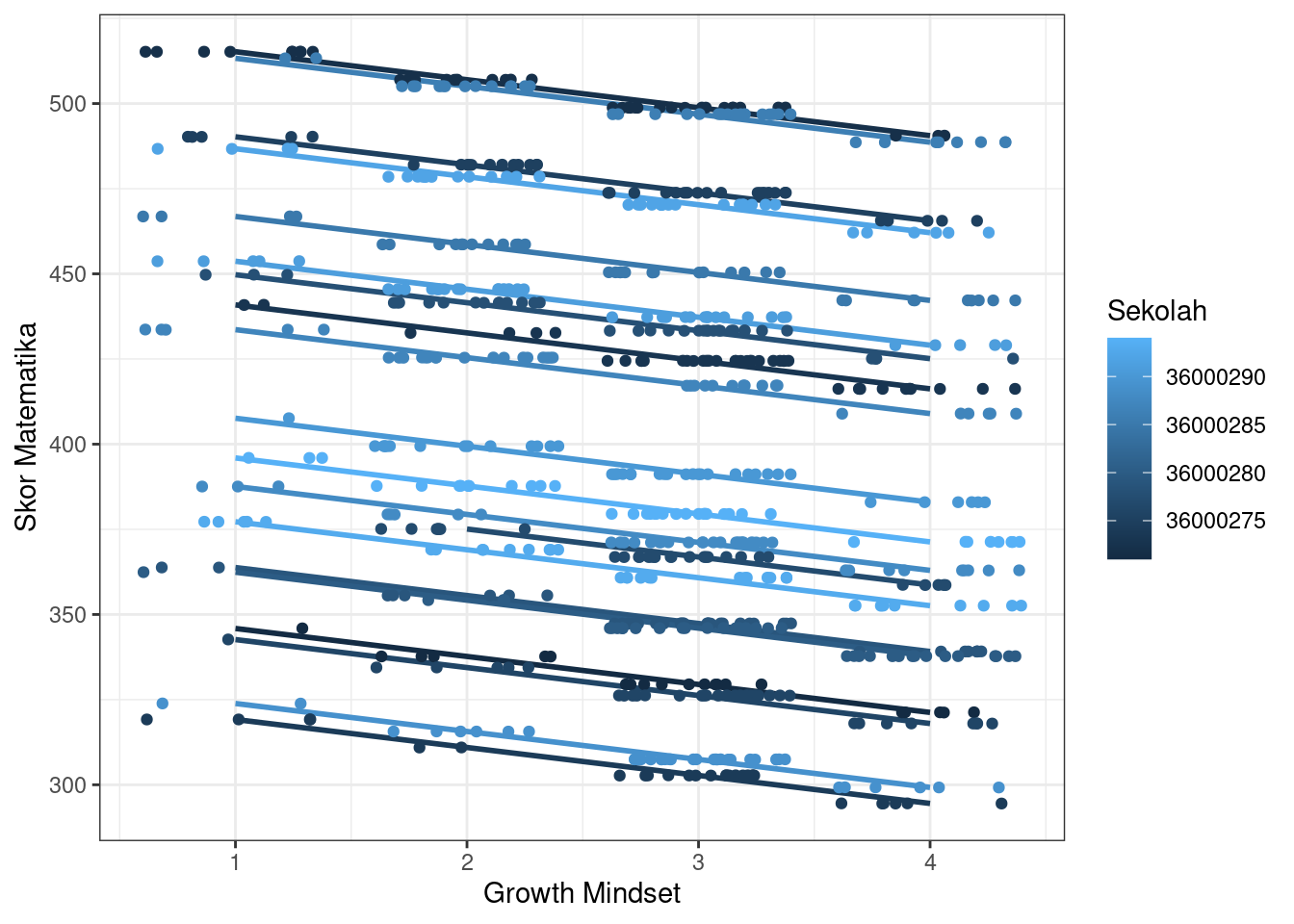
14 Random Slope
14.1 Intuisi Random Slope
Model sebelumnya membuat asumsi bahwa pengaruh growth mindset adalah sama di semua sekolah (itu sebabnya garisnya paralel).
Bagaimana jika satu skor growth mindset lebih “efektif” di beberapa sekolah daripada yang lain dalam meningkatkan skor matematika.
Pada titik ini random slope diperlukan.
Kita memperoleh koefisien baru yang menggambarkan perbedaan antar sekolah dalam pengaruh growth mindset terhadap skor matematika.
14.2 Estimasi Random Slope
# model with random slope
m2 <- lmer(math ~ 1 + growth +
(1 + growth | CNTSCHID),
data = skor)
# print results
summary(m2)Linear mixed model fit by REML ['lmerMod']
Formula: math ~ 1 + growth + (1 + growth | CNTSCHID)
Data: skor
REML criterion at convergence: 7900.8
Scaled residuals:
Min 1Q Median 3Q Max
-4.0670 -0.6649 0.0295 0.6340 3.3370
Random effects:
Groups Name Variance Std.Dev. Corr
CNTSCHID (Intercept) 5277.12 72.644
growth 73.29 8.561 -0.55
Residual 2525.62 50.256
Number of obs: 733, groups: CNTSCHID, 20
Fixed effects:
Estimate Std. Error t value
(Intercept) 420.311 17.569 23.924
growth -8.054 2.984 -2.699
Correlation of Fixed Effects:
(Intr)
growth -0.60614.3 Estimasi Random Slope
tab_model(m2, show.icc = TRUE)| math | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 420.31 | 385.82 – 454.80 | <0.001 |
| growth | -8.05 | -13.91 – -2.20 | 0.007 |
| Random Effects | |||
| σ2 | 2525.62 | ||
| τ00 CNTSCHID | 5277.12 | ||
| τ11 CNTSCHID.growth | 73.29 | ||
| ρ01 CNTSCHID | -0.55 | ||
| ICC | 0.61 | ||
| N CNTSCHID | 20 | ||
| Observations | 733 | ||
| Marginal R2 / Conditional R2 | 0.007 / 0.616 | ||
14.4 Interpretasi Random Slope
- Fixed effect growth mindset mengecil dibanding model 1 dan kita mempunyai koefisien baru random effect.
- Varian random slope untuk tahun pendidikan adalah 73.29.
14.5 Sebaran Random Slope
skor$m2 <- predict(m2)
# visualize the predictions based on our model
skor %>%
ggplot(aes(growth, m2)) +
geom_smooth(se = F, method = lm, size = 2) +
geom_jitter()+
stat_smooth(aes(color = CNTSCHID, group = CNTSCHID),
geom = "line", alpha = 0.4, size = 1) +
theme_bw() +
guides(color = F) +
labs(x = "Growth Mindset",
y = "Skor Matematika",
color = "Sekolah")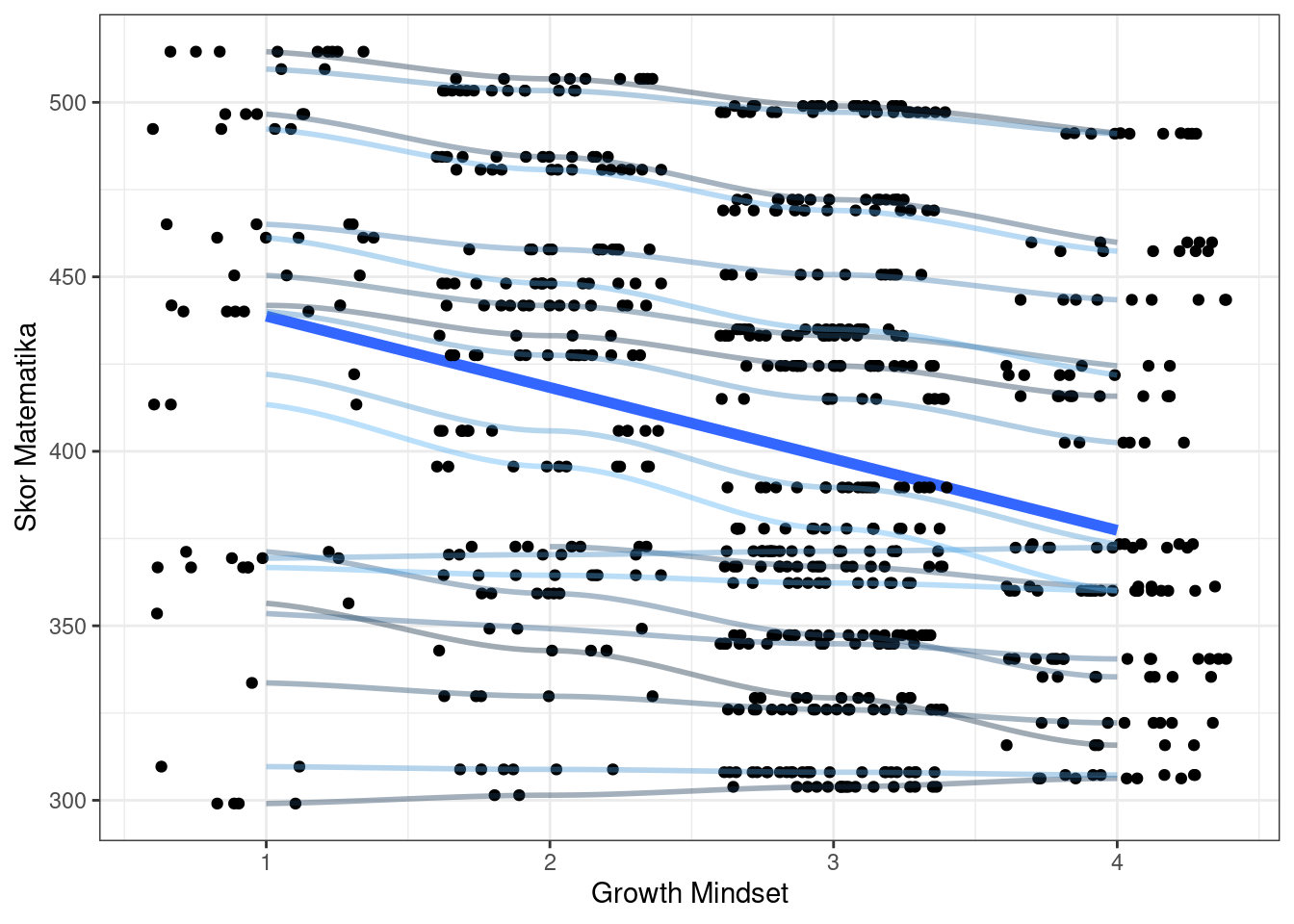
Fixed effect yaitu -8.054, tetapi setiap sekolah memiliki slope yang beragam.
14.6 Sebaran intercept
# another way to see random effect
qqmath(ranef(m2, condVar = TRUE))$CNTSCHID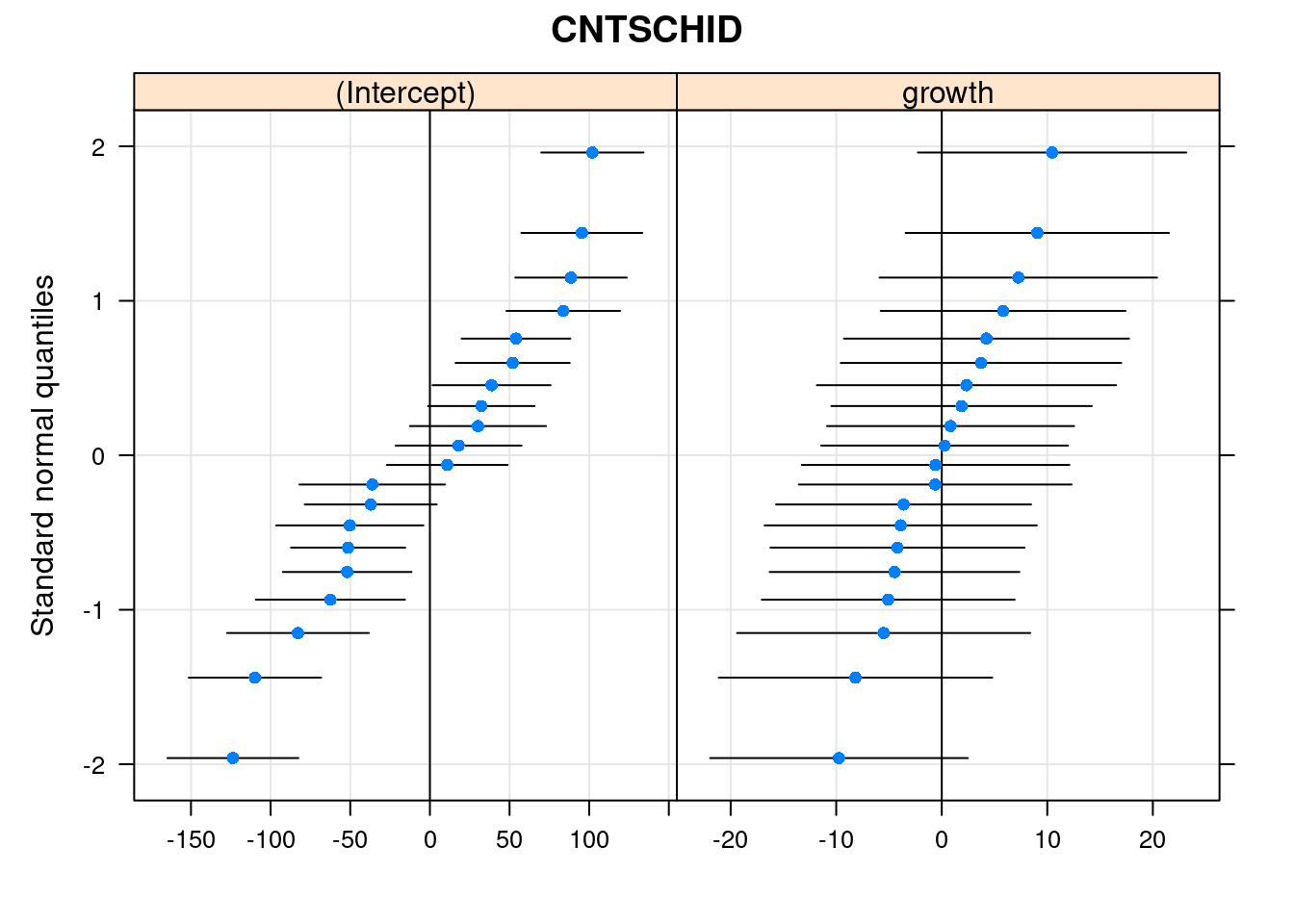
Grafik menunjukkan bagaimana pengaruh growth mindset bervariasi di setiap sekolah.
14.7 Random Effects
# yet another way to look at the random effects
# save coefficients
coefs_m2 <- coef(m2)
# print random effects and best line
coefs_m2$CNTSCHID %>%
mutate(CNTSCHID = rownames(coefs_m2$CNTSCHID)) %>%
ggplot(aes(growth, `(Intercept)`, label = CNTSCHID)) +
geom_point() +
geom_smooth(se = F, method = lm) +
geom_label(nudge_y = 0.15, alpha = 0.5) +
theme_bw() +
labs(x = "Slope", y = "Intercept")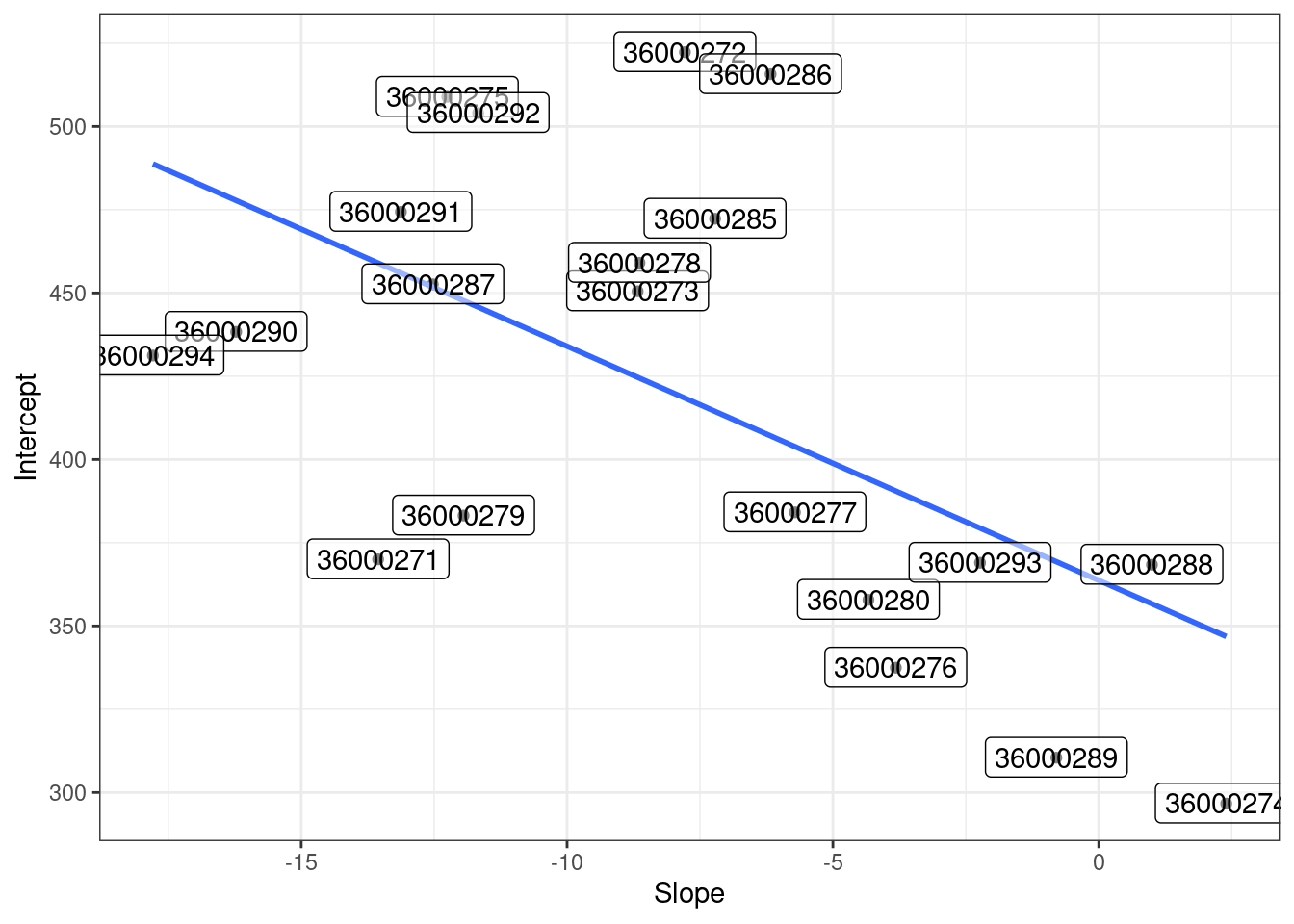
14.8 Interpretasi random effects
Grafik menunjukkan bahwa beberapa sekolah memiliki memiliki skor matematika yang tinggi tetapi memiliki efek yang rendah pada outcome dan sebaliknya.
Garis biru mewakili hubungan antara intersep acak dan kemiringan dengan koefisien sebesar 0.6. Hal ini menunjukkan bahwa semakin kecil fixed mindset, semakin tinggi skor matematika.
15 Refleksi untuk penelitian lanjut
15.1 Penerapan
- Eksperimen
- Meta analisis
- Survey
- Multilevel SEM
- Penelitian longitudinal
15.2 Refleksi akhir
- Analisis multilevel membantu mengurangi kesalahan dalam pembuatan kesimpulan
- Pentingnya memperhatikan konteks dalam studi psikologi
- Pemanfaatan data skala besar untuk penelitian psikologi
- Dalam pembuatan kebijakan analisis multilevel dapat digunakan untuk kebijakan yang lebih presisi.